Revisions for Thermal photography
| 67 | sara |
March 16, 2012 22:46
| over 12 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
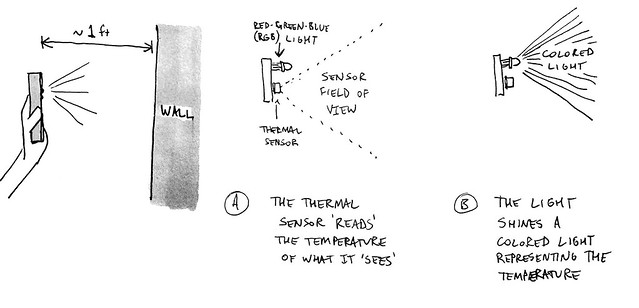
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Using a Thermal FlashlightTo capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page.
Building your ownParts list For a Thermal Flashlight with 3.6 V Melexis Sensor and Common Anode LED.
Alternative variations of the Flashlight can be made with a 5.5V Melexis Sensor and Common Cathode LED. For the 5.5 V sensor follow this diagram: http://publiclaboratory.org/notes/sara/2-7-2012/circuit-diagram-5v-melexis-sensor For the common cathode circuit board follow this diagram: http://publiclaboratory.org/notes/warren/2-11-2012/common-cathode-variant-thermal-flashlight-code Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch:
Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 66 | sara |
March 16, 2012 22:41
| over 12 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Using a Thermal FlashlightTo capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page.
Building your ownParts list For a Thermal Flashlight with 3.6 V Melexis Sensor and Common Anode LED.
Alternative variations of the Flashlight can be made with a 5.5V Melexis Sensor and Common Cathode LED. For the 5.5 V sensor follow this diagram: http://publiclaboratory.org/notes/sara/2-7-2012/circuit-diagram-5v-melexis-sensor For the common cathode circuit board follow this diagram: http://publiclaboratory.org/notes/warren/2-11-2012/common-cathode-variant-thermal-flashlight-code Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch:
Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 65 | sara |
March 16, 2012 22:39
| over 12 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Using a Thermal FlashlightTo capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page.
Building your ownParts list For a Thermal Flashlight with 3.6 V Melexis Sensor and Common Anode LED.
Alternative variations of the Flashlight can be made with a 5.5V Melexis Sensor and Common Cathode LED. For the 5.5 V sensor follow this diagram: http://publiclaboratory.org/notes/sara/2-7-2012/circuit-diagram-5v-melexis-sensor For the common anode circuit board follow this diagram: In design. Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch:
Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 64 | warren |
March 14, 2012 01:24
| over 12 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Using a Thermal FlashlightTo capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page.
Building your ownParts list For a Thermal Flashlight with 3.6 V Melexis Sensor and Common Cathode LED.
Alternative variations of the Flashlight can be made with a 5.5V Melexis Sensor and Common Anode LED. For the 5.5 V sensor follow this diagram: http://publiclaboratory.org/notes/sara/2-7-2012/circuit-diagram-5v-melexis-sensor For the common anode circuit board follow this diagram: In design. Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch:
Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 63 | sara |
March 12, 2012 19:59
| over 12 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Using a Thermal FlashlightTo capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page.
Building your ownParts list For a Thermal Flashlight with 3.6 V Melexis Sensor and Common Cathode LED.
Alternative variations of the Flashlight can be made with a 5.5V Melexis Sensor and Common Anode LED. For the 5.5 V sensor follow this diagram: http://publiclaboratory.org/notes/sara/2-7-2012/circuit-diagram-5v-melexis-sensor For the common anode circuit board follow this diagram: In design. Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch:
Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 62 | sara |
March 12, 2012 19:56
| over 12 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Using a Thermal FlashlightTo capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page.
Building your ownParts list For a Thermal Flashlight with 3.6 V Melexis Sensor and Common Cathode LED.
Alternative variations of the Flashlight can be made with a 5.5V Melexis Sensor and Common Anode LED. For the 5.5 V sensor follow this diagram: http://publiclaboratory.org/notes/sara/2-7-2012/circuit-diagram-5v-melexis-sensor For the common anode circuit board follow this diagram: In design. Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch:
Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 61 | sara |
March 12, 2012 19:47
| over 12 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Using a Thermal FlashlightTo capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page.
Building your ownParts list For a Thermal Flashlight with 3.6 V Melexis Sensor and Common Cathode LED.
Alternative variations of the Flashlight can be made with a 5.5V Melexis Sensor and Common Anode LED. For the 5.5 V sensor follow this diagram: http://publiclaboratory.org/notes/sara/2-7-2012/circuit-diagram-5v-melexis-sensor For the common anode circuit board follow this diagram: In design. Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch:
Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 60 | sara |
March 12, 2012 19:46
| over 12 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Using a Thermal FlashlightTo capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page.
Building your ownParts list For a Thermal Flashlight with 3.6 V Melexis Sensor and Common Cathode LED.
Alternative variation of the Flashlight can be made with a 5.5V Melexis Sensor and Common Anode LED. For the 5.5 V sensor follow this diagram: http://publiclaboratory.org/notes/sara/2-7-2012/circuit-diagram-5v-melexis-sensor For the common anode circuit board follow this diagram: In design. Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch:
Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 59 | warren |
February 29, 2012 18:55
| over 12 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Using a Thermal FlashlightTo capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page.
Building your ownParts list
Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch:
Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 58 | warren |
February 16, 2012 20:17
| almost 13 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
To capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page. Building your ownParts list
Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch:
Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 57 | warren |
February 16, 2012 20:16
| almost 13 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
To capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page. Building your ownParts list
Links to purchasing equipment: Consumable Parts:
If you are starting an electronics kit from scratch: * a 40Watt soldering Iron (if you want it to be permanent otherwise duct tape or Velcro works temporarily) * hookup wire (solid not stranded- 22 or 24 gauge, you can get this at Radio Shack) * pliers called "wire strippers" to get the plastic wrap off the hookup wire (can get at Radio Shack) * solder for 40Watt iron, lead-free. * a breadboard (1 per flashlight). If you aren't soldering: http://www.adafruit.com/products/64. If you are soldering: https://www.adafruit.com/products/571. * a USB cable to connect the arduino to the computer via USB for power 5Volts (can get at Radio Shack) * household sponge for cleaning solder off tip * 9 volt battery with connector wires (can get at Radio Shack- 1 per flashlight) Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 56 | Shannon |
February 08, 2012 15:32
| almost 13 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
To capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page. Building your ownParts list
Links to purchasing equipment: Consumable Parts: * LEDs (1 per flashlight, but they sell as a pack of 25): http://www.sparkfun.com/products/10818 * Arduino Uno (1 per flashlight): http://www.sparkfun.com/products/11021 * Capicator (1 per flashlight): http://www.sparkfun.com/products/8375 * Resistor pack (this pack has a 180 ohm resistor which we found other packs not to have): http://www.eio.com/p-19326-velleman-kres-e12-pack-of-610-e12-series-resistors.aspx * 5.5v infra red thermometer (1 per flashlight): http://www.futureelectronics.com/en/technologies/semiconductors/analog/sensors/temperature/Pages/6266423-MLX90614ESF-AAA.aspx?IM=1. If you use this sensor, follow this diagram: http://publiclaboratory.org/notes/sara/2-7-2012/circuit-diagram-5v-melexis-sensor If you are starting an electronics kit from scratch: * a 40Watt soldering Iron (if you want it to be permanent otherwise duct tape or Velcro works temporarily) * hookup wire (solid not stranded- 22 or 24 gauge, you can get this at Radio Shack) * pliers called "wire strippers" to get the plastic wrap off the hookup wire (can get at Radio Shack) * solder for 40Watt iron, lead-free. * a breadboard (1 per flashlight). If you aren't soldering: http://www.adafruit.com/products/64. If you are soldering: https://www.adafruit.com/products/571. * a USB cable to connect the arduino to the computer via USB for power 5Volts (can get at Radio Shack) * household sponge for cleaning solder off tip * 9 volt battery with connector wires (can get at Radio Shack- 1 per flashlight) Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 55 | Shannon |
February 07, 2012 16:12
| almost 13 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
To capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page. Building your ownParts list
Links to purchasing equipment: Consumable Parts: * LEDs (1 per flashlight, but they sell as a pack of 25): http://www.sparkfun.com/products/10818 * Arduino Uno (1 per flashlight): http://www.sparkfun.com/products/11021 * Capicator (1 per flashlight): http://www.sparkfun.com/products/8375 * Resistor pack (this pack has a 180 ohm resistor which we found other packs not to have): http://www.eio.com/p-19326-velleman-kres-e12-pack-of-610-e12-series-resistors.aspx * 5.5v infra red thermometer (1 per flashlight): http://www.futureelectronics.com/en/technologies/semiconductors/analog/sensors/temperature/Pages/6266423-MLX90614ESF-AAA.aspx?IM=1 If you are starting an electronics kit from scratch: * a 40Watt soldering Iron (if you want it to be permanent otherwise duct tape or Velcro works temporarily) * hookup wire (solid not stranded- 22 or 24 gauge, you can get this at Radio Shack) * pliers called "wire strippers" to get the plastic wrap off the hookup wire (can get at Radio Shack) * solder for 40Watt iron, lead-free. * a breadboard (1 per flashlight). If you aren't soldering: http://www.adafruit.com/products/64. If you are soldering: https://www.adafruit.com/products/571. * a USB cable to connect the arduino to the computer via USB for power 5Volts (can get at Radio Shack) * household sponge for cleaning solder off tip * 9 volt battery with connector wires (can get at Radio Shack- 1 per flashlight) Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 54 | Shannon |
February 07, 2012 16:10
| almost 13 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
To capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page. Building your ownParts list
Links to purchasing equipment: Consumable Parts: * LEDs (1 per flashlight, but they sell as a pack of 25): http://www.sparkfun.com/products/10818 * Arduino Uno (1 per flashlight): http://www.sparkfun.com/products/11021 * Capicator (1 per flashlight): http://www.sparkfun.com/products/8375 * Resistor pack (this pack has a 180 ohm resistor which we found other packs not to have): http://www.eio.com/p-19326-velleman-kres-e12-pack-of-610-e12-series-resistors.aspx * 5.5v infra red thermometer (1 per flashlight): http://www.futureelectronics.com/en/technologies/semiconductors/analog/sensors/temperature/Pages/6266423-MLX90614ESF-AAA.aspx?IM=1 If you are starting an electronics kit from scratch: * a 40Watt soldering Iron (if you want it to be permanent otherwise duct tape or Velcro works temporarily) * hookup wire (solid not stranded- 22 or 24 gauge, you can get this at Radio Shack) * pliers called "wire strippers" to get the plastic wrap off the hookup wire (can get at Radio Shack) * solder for 40Watt iron, lead-free. * a breadboard. If you aren't soldering: http://www.adafruit.com/products/64. If you are soldering: https://www.adafruit.com/products/571. * a USB cable to connect the arduino to the computer via USB for power 5Volts (can get at Radio Shack) * household sponge for cleaning solder off tip * 9 volt battery with connector wires (can get at Radio Shack) Cost: ~$40-$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 53 | warren |
December 31, 2011 21:35
| almost 13 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
To capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page. Building your ownParts list
Cost: ~$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 52 | warren |
December 31, 2011 21:14
| almost 13 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
To capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page. Building your ownParts list
Cost: ~$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 51 | liz |
December 23, 2011 17:14
| almost 13 years ago
ApplicationsThermal imaging can be used to document heat/AC leaks from insulation gaps on a building's facade, reveal warmer ground water inflows (either fresh or chemical-laden) or "thermal pollution" from industrial processes entering ocean-temperature waterbodies, as well as identify areas on the human body experiencing infection or stress (includes epidemiological applications). Community applications so far include both a "heat-busters" program in East Harlem and a "forensic" water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
To capture the light painting over time, we have been using timelapse photography or GlowDoodle, as seen in the top image on this page. Building your ownParts list
Cost: ~$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 50 | warren |
December 21, 2011 22:47
| almost 13 years ago
ApplicationsThere are two primary types of environmental investigations that are driving the development of DIY thermal imaging tools and methods: a "heat-busters" program in East Harlem, and a near-forensic-level water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Building your ownParts list
Cost: ~$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 49 | warren |
December 19, 2011 13:39
| almost 13 years ago
ApplicationsThere are two primary types of environmental investigations that are driving the development of DIY thermal imaging tools and methods: a "heat-busters" program in East Harlem, and a near-forensic-level water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Building your ownParts list
Cost: ~$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert | |
| 48 | warren |
December 18, 2011 21:15
| almost 13 years ago
ApplicationsThere are two primary types of environmental investigations that are driving the development of DIY thermal imaging tools and methods: a "heat-busters" program in East Harlem, and a near-forensic-level water quality monitoring program in the Gowanus Canal. ApproachesThere are three prototypes in development:
Problem"FLIR" cameras can produce images such as the one below, and are typically used to identify heat leaks, but even low-resolution FLIR cameras can cost thousands of dollars. Our goal is to make this kind of investigation (and the potential savings) cheap, easy, fun, and informative for those of us without $10k in our pockets.
Thermal FlashlightThe first approach results in a kind of "light painting" -- a color heatmap overlaid directly onto the scene. This is the simplest, cheapest, and to date, most effective way we have developed of measuring heat leaks or cool leaks indoors and outdoors. Simply put, the "flashlight" puts out red light if it's pointed at something hot (default 75 deg F or more) and blue light if it's pointed at something cold *(default 60 deg F or less):
Building your ownParts list
Cost: ~$60 These research notes will be integrated into this page to provide instructions on building and using your own thermal flashlight:
Several meetups have been organized to build and test thermal flashlights, at RISD (Providence, RI) and in Brooklyn, NY. We are organizing one now in Somerville, MA:
Thermal flashlight heatmaps |
Revert |