Leaflet.DistortableImage (LDI) -
"A Leaflet extension to distort images -- "rubbersheeting" -- for the MapKnitter.org (src) image georectification service by Public Lab. Leaflet.DistortableImage allows for perspectival distortions of images, client-side, using CSS3 transformations in the DOM." - README
Now that we've introduced LDI, this post should help those that are not GIS mapping enthusiasts get to know the plugin (and potentially make you want to become mapping enthusiasts - highly recommend).
Key concepts
LDI allows for perspectival distortions of aerial images over a flat, projected map. It is key for georectification.
Perspectival distortions?
Try out the distort tool below (3rd tool from the left).
Aerial images typically have some level of distortion resulting from the camera perspective. A perfectly perpendicular photo is difficult to achieve due to many factors, and significantly more so with balloon mapping as you might envision. (wind, camera swinging, etc.)
Projective transformation
We correct for camera perspective distortion by using a projective transformation. Specifically, we calculate a 4*4 projective transformation matrix mapping each corner of the aerial photograph to a geographic coordinate on the map.
An image can be transformed in 2D (planar) using various transformation rules:
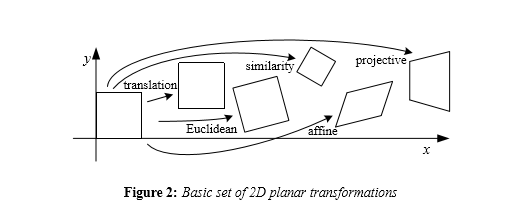
These transformations can all be described by transformation matrices which map the untransformed image to the transformed one.
An affine transformation would have been sufficient for rotation and scaling, but distortion requires a projective transformation which does not preserve parallelism.
Preserving parallelism limits affine transformations in a way. If you want to do perspective, you should do a projective transformation.
Georectification
Ultimately, this transformation allows us to neatly fit images taken from multiple perspectives into a common map coordinate system, a process called georectification.
Below is a great visual example of an image being rectified over a plane:
Set of 2D images. The original images are taken from different perspectives (row 1). Using systematic transformations (rows 2 and 3), we are able to transform both images such that corresponding points are on the same horizontal scan lines (row 4).

Translated to code
The projective transformation functionality achieved via the #_calculateProjectiveTransform method is the core of LDI:
_calculateProjectiveTransform: function(latLngToCartesian) {
var offset = latLngToCartesian(this.getCorner(0));
var w = this.getElement().offsetWidth || 500;
var h = this.getElement().offsetHeight || 375;
var c = [];
for (j = 0; j < 4; j++) {
c.push(latLngToCartesian(this.getCorner(j))._subtract(offset));
}
return L.MatrixUtil.general2DProjection(
0, 0, c[0].x, c[0].y,
w, 0, c[1].x, c[1].y,
0, h, c[2].x, c[2].y,
w, h, c[3].x, c[3].y
);
},
The process coded above is as follows:
- We remove the core Leaflet
translate3dtransformation. - We use the cartesian coordinates of the image's top-left corner as the base offset.
- We subtract the base offset from the cartesian coordinates of each of the image's 4 corners, placing the image at a standard 0, 0 coordinate in the top-left corner of the map.
- With the image being projected at the origin of the map, we compute the homogenous transformation matrix. Using homogenous coordinates allows us to compose multiple transformations (rotation, scaling, distortion) all in a single matrix multiplication.
- This matrix is then handed off to the
matrix3dCSS3 function, which applies the transformation. It maps a 3x3 projective matrix to 4x4 homogenous coordinates. - We re-apply the core Leaflet
translate3dtransformation we stripped in step 1. - Every time you distort the image or change the zoom level of the map, this function is triggered again to recalculate.
Contributing:
You can help document this functionality by writing specs for it - please visit this issue.

1 Comments
Love this, and great diagrams!!! Thanks, Sasha!!
Reply to this comment...
Log in to comment
Login to comment.